Consider Again the Problem of Merging K Sorted Length-n Arrays

Giving k sorted arrays, each of size Northward, the chore is to merge them into a single sorted assortment.

Examples:

          Input:          arr[][] = {{5, vii, xv, 18},                    {one, 8, 9, 17},                    {1, 4, 7, vii}}          Output:          {ane, ane, iv, 5, seven, vii, 7, 8, 9, 15, 17, 18}          Input:          arr[][] = {{3, 2, 1}                    {6, 5, 4}}          Output:          {1, 2, three, 4, 5, half-dozen}

Prerequisite: Merge Sort
Simple Arroyo: A simple solution is to append all the arrays one after some other and sort them.

C++fourteen

#include <$.25/stdc++.h>

using namespace std;

#define North iv

void merge_and_sort(

vector< int > &output, vector<vector< int >> arr,

int due north, int m)

{

for ( int i = 0; i < thousand; i++) {

for ( int j = 0; j < northward; j++) {

output[(i * n) + j] = arr[i][j];

}

}

sort(output.begin(), output.terminate());

}

int main()

{

vector<vector< int >> arr = { { 5, 7, xv, 18 },

{ 1, 8, 9, 17 },

{ 1, 4, seven, 7 } };

int n = N;

int k = arr.size();

vector< int > output(n*g);

merge_and_sort(output, arr, n, k);

for ( int i = 0; i < north * k; i++)

cout << output[i] << " " ;

return 0;

}

Java

import java.util.*;

class GFG

{

static int N = iv ;

static void merge_and_sort( int output[], int arr[][],

int n, int yard)

{

for ( int i = 0 ; i < k; i++)

{

for ( int j = 0 ; j < n; j++)

{

output[i * n + j] = arr[i][j];

}

}

Arrays.sort(output);

}

public static void primary(String[] args)

{

int arr[][] = { { 5 , 7 , 15 , 18 },

{ ane , eight , 9 , 17 },

{ 1 , 4 , 7 , vii } };

int north = Due north;

int grand = arr.length;

int output[] = new int [n * k];

merge_and_sort(output, arr, n, thou);

for ( int i = 0 ; i < n * k; i++)

System.out.print(output[i] + " " );

}

}

Python3

Due north = 4

def merge_and_sort(output, arr, n, k):

for i in range (k):

for j in range (n):

output[i * n + j] = arr[i][j];

output.sort()

if __name__ = = '__main__' :

arr = [ [ 5 , 7 , 15 , 18 ],

[ ane , 8 , ix , 17 ],

[ i , 4 , vii , seven ] ];

northward = N;

k = len (arr)

output = [ 0 for i in range (n * 1000)]

merge_and_sort(output, arr, n, one thousand);

for i in range (northward * one thousand):

print (output[i], stop = ' ' )

C#

using System;

grade GFG

{

static int N = iv;

static void merge_and_sort( int [] output, int [,] arr,

int n, int g)

{

for ( int i = 0; i < k; i++)

{

for ( int j = 0; j < n; j++)

{

output[i * n + j] = arr[i,j];

}

}

Array.Sort(output);

}

static void Main()

{

int [,] arr = { { five, vii, 15, 18 },

{ one, 8, 9, 17 },

{ 1, four, 7, seven } };

int due north = N;

int k = arr.GetLength(0);

int [] output = new int [northward * k];

merge_and_sort(output, arr, n, yard);

for ( int i = 0; i < northward * one thousand; i++)

Panel.Write(output[i] + " " );

}

}

Javascript

<script>

allow Northward = 4;

function merge_and_sort(output, arr, northward, k)

{

for (let i = 0; i < k; i++)

{

for (permit j = 0; j < n; j++)

{

output[i * north + j] = arr[i][j];

}

}

output.sort( function (a, b){ render a - b});

}

let arr = [ [ v, seven, 15, 18 ],

[ 1, eight, nine, 17 ],

[ 1, iv, vii, seven ] ];

let n = N;

let k = 3;

let output = new Array(northward * k);

merge_and_sort(output, arr, n, k);

for (let i = 0; i < n * k; i++)

document.write(output[i] + " " );

</script>

Output:

ane 1 4 v 7 vii 7 8 9 fifteen 17 xviii

Complexity Analysis:

• Time Complexity: O(Due north*g*log(N*k)).
  The size of all elements is n*yard and then the time complexity is O(N*k * log(N*k))
• Space Complexity: O(N*chiliad).
  To store the output assortment O(N*k) space is required.

Efficient Solution :
Approach: The idea becomes clear once we starting time looking at the 1000 arrays as the intermediate state of the merge sort algorithm.
Since there are k arrays that are already sorted, merge the m arrays. Create a recursive function which will take k arrays and divide them into 2 parts and call the function recursively with each half. The base cases are when the value of k is less than 3.
Encounter this article to merge two arrays in O(n) fourth dimension.

Algorithm:

1. Initialize the output array with the size N*k.
2. Call the function divide. Let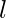and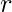represent the range of arrays that are to be merged and thus vary betwixt 0 to k-1.
3. At each step, we call the left and correct half of the range recursively so that, they will be sorted and stored in the output array.
4. After that, we merge the left and right one-half. For merging, we demand to make up one's mind the range of indexes for the left and right halves in the output assortment. We can easily observe that.
   1. Left function will first from the alphabetize l * n of the output assortment.
   2. Similarly, right part volition get-go from the index ((l + r) / two + 1) * north of the output array.

C++

#include<bits/stdc++.h>

#ascertain northward four

using namespace std;

void merge( int l, int r, vector< int >& output)

{

int l_in = l * n, r_in

= ((l + r) / 2 + 1) * n;

int l_c = ((l + r) / ii - l + 1) * n;

int r_c = (r - (fifty + r) / 2) * n;

int l_arr[l_c], r_arr[r_c];

for ( int i = 0; i < l_c; i++)

l_arr[i] = output[l_in + i];

for ( int i = 0; i < r_c; i++)

r_arr[i] = output[r_in + i];

int l_curr = 0, r_curr = 0;

int in = l_in;

while (

l_curr + r_curr < l_c + r_c) {

if (

r_curr == r_c

|| (l_curr != l_c

&& l_arr[l_curr] < r_arr[r_curr]))

output[in]

= l_arr[l_curr],

l_curr++, in++;

else

output[in]

= r_arr[r_curr],

r_curr++, in++;

}

}

void divide( int fifty, int r, vector< int >& output,

vector<vector< int >> arr)

{

if (fifty == r) {

for ( int i = 0; i < n; i++)

output[l * northward + i] = arr[50][i];

return ;

}

split(l, (l + r) / 2,

output, arr);

divide((l + r) / ii + i, r,

output, arr);

merge(l, r, output);

}

int main()

{

vector<vector< int >> arr = { { v, 7, xv, 18 },

{ i, viii, 9, 17 },

{ 1, 4, 7, vii } };

int k = arr.size();

vector< int > output(n*k);

divide(0, k - 1, output, arr);

for ( int i = 0; i < north * k; i++)

cout << output[i] << " " ;

return 0;

}

Java

import java.util.*;

course GFG {

static int n = iv ;

static void merge(

int 50, int r, int [] output)

{

int l_in = l * n, r_in

= ((fifty + r) / two + 1 ) * n;

int l_c = ((l + r) / two - fifty + ane ) * due north;

int r_c = (r - (l + r) / 2 ) * n;

int l_arr[] = new int [l_c],

r_arr[] = new int [r_c];

for ( int i = 0 ; i < l_c; i++)

l_arr[i] = output[l_in + i];

for ( int i = 0 ; i < r_c; i++)

r_arr[i] = output[r_in + i];

int l_curr = 0 , r_curr = 0 ;

int in = l_in;

while (l_curr + r_curr < l_c + r_c) {

if (

r_curr == r_c

|| (l_curr != l_c

&& l_arr[l_curr] < r_arr[r_curr])) {

output[in] = l_arr[l_curr];

l_curr++;

in++;

}

else {

output[in] = r_arr[r_curr];

r_curr++;

in++;

}

}

}

static void split( int l, int r, int [] output,

int arr[][])

{

if (l == r) {

for ( int i = 0 ; i < due north; i++)

output[l * n + i] = arr[l][i];

return ;

}

separate(fifty, (l + r) / 2 , output, arr);

split up((l + r) / 2 + i , r, output, arr);

merge(fifty, r, output);

}

public static void main(Cord[] args)

{

int arr[][] = { { v , seven , fifteen , eighteen },

{ 1 , viii , ix , 17 },

{ 1 , four , seven , 7 } };

int yard = arr.length;

int [] output = new int [n * k];

separate( 0 , chiliad - one , output, arr);

for ( int i = 0 ; i < n * k; i++)

Arrangement.out.print(output[i] + " " );

}

}

Python3

north = 4 ;

def merge(l, r, output) :

l_in = l * n ;

r_in = ((l + r) / / ii + 1 ) * n;

l_c = ((l + r) / / 2 - l + one ) * northward;

r_c = (r - (l + r) / / two ) * northward;

l_arr = [ 0 ] * l_c; r_arr = [ 0 ] * r_c;

for i in range (l_c) :

l_arr[i] = output[l_in + i];

for i in range (r_c) :

r_arr[i] = output[r_in + i];

l_curr = 0 ; r_curr = 0 ;

in1 = l_in;

while (l_curr + r_curr < l_c + r_c) :

if (r_curr = = r_c or (l_curr ! = l_c and

l_arr[l_curr] < r_arr[r_curr])) :

output[in1] = l_arr[l_curr];

l_curr + = 1 ; in1 + = i ;

else :

output[in1] = r_arr[r_curr];

r_curr + = 1 ; in1 + = 1 ;

def carve up(l, r, output, arr) :

if (l = = r) :

for i in range (n) :

output[l * n + i] = arr[l][i];

return ;

split up(50, (l + r) / / 2 , output, arr);

dissever((50 + r) / / ii + 1 , r, output, arr);

merge(fifty, r, output);

if __name__ = = "__main__" :

arr = [[ 5 , 7 , 15 , xviii ],

[ 1 , 8 , 9 , 17 ],

[ 1 , iv , 7 , seven ]];

g = len (arr);

output = [ 0 ] * (northward * chiliad);

divide( 0 , thou - 1 , output, arr);

for i in range (northward * g) :

print (output[i], end = " " );

C#

using System;

class GFG {

static int n = 4;

static void merge( int fifty, int r, int [] output)

{

int l_in = l * n, r_in = ((50 + r) / 2 + 1) * n;

int l_c = ((l + r) / two - l + ane) * n;

int r_c = (r - (l + r) / 2) * n;

int [] l_arr = new int [l_c];

int [] r_arr = new int [r_c];

for ( int i = 0; i < l_c; i++)

l_arr[i] = output[l_in + i];

for ( int i = 0; i < r_c; i++)

r_arr[i] = output[r_in + i];

int l_curr = 0, r_curr = 0;

int index = l_in;

while (l_curr + r_curr < l_c + r_c) {

if (r_curr == r_c || (l_curr != l_c && l_arr[l_curr] < r_arr[r_curr])) {

output[alphabetize] = l_arr[l_curr];

l_curr++;

alphabetize++;

}

else {

output[index] = r_arr[r_curr];

r_curr++;

alphabetize++;

}

}

}

static void separate( int l, int r, int [] output,

int [, ] arr)

{

if (l == r) {

for ( int i = 0; i < n; i++)

output[l * n + i] = arr[l, i];

return ;

}

split(l, (50 + r) / ii, output, arr);

split up((l + r) / 2 + i, r, output, arr);

merge(l, r, output);

}

public static void Master(Cord[] args)

{

int [, ] arr = { { 5, 7, xv, 18 },

{ 1, 8, 9, 17 },

{ 1, 4, 7, 7 } };

int k = arr.GetLength(0);

int [] output = new int [n * k];

separate(0, one thousand - 1, output, arr);

for ( int i = 0; i < n * k; i++)

Console.Write(output[i] + " " );

}

}

PHP

<?php

$n = 4;

function merge( $l , $r , & $output )

{

global $northward ;

$l_in = $l * $northward ;

$r_in = ((int)(( $50 + $r ) / 2) + one) * $northward ;

$l_c = (int)(((( $fifty + $r ) / 2) - $l + 1) * $n );

$r_c = ( $r - (int)(( $50 + $r ) / 2)) * $n ;

$l_arr = array_fill (0, $l_c , 0);

$r_arr = array_fill (0, $r_c , 0);

for ( $i = 0; $i < $l_c ; $i ++)

$l_arr [ $i ] = $output [ $l_in + $i ];

for ( $i = 0; $i < $r_c ; $i ++)

$r_arr [ $i ] = $output [ $r_in + $i ];

$l_curr = 0;

$r_curr = 0;

$in = $l_in ;

while ( $l_curr + $r_curr < $l_c + $r_c )

{

if ( $r_curr == $r_c || ( $l_curr != $l_c &&

$l_arr [ $l_curr ] < $r_arr [ $r_curr ]))

{

$output [ $in ] = $l_arr [ $l_curr ];

$l_curr ++; $in ++;

}

else

{

$output [ $in ] = $r_arr [ $r_curr ];

$r_curr ++; $in ++;

}

}

}

role divide( $50 , $r , & $output , $arr )

{

global $n ;

if ( $l == $r )

{

for ( $i = 0; $i < $n ; $i ++)

$output [ $50 * $n + $i ] = $arr [ $l ][ $i ];

return ;

}

divide( $50 , (int)(( $l + $r ) / 2), $output , $arr );

split up((int)(( $l + $r ) / ii) + 1, $r , $output , $arr );

merge( $l , $r , $output );

}

$arr = array ( array ( 5, 7, 15, 18 ),

array ( one, 8, 9, 17 ),

assortment ( 1, 4, 7, 7 ));

$k = count ( $arr );

$output = array_fill (0, $n * $k , 0);

divide(0, $1000 - 1, $output , $arr );

for ( $i = 0; $i < $n * $k ; $i ++)

print ( $output [ $i ] . " " );

?>

Javascript

<script>

var n = 4;

function merge(l, r, output)

{

var l_in = l * n,

r_in = (parseInt((l + r) / 2) + one) * northward;

var l_c = (parseInt((l + r) / 2) - l + i) * northward;

var r_c = (r - parseInt((l + r) / 2)) * north;

var l_arr = Assortment(l_c), r_arr = Assortment(r_c);

for ( var i = 0; i < l_c; i++)

l_arr[i] = output[l_in + i];

for ( var i = 0; i < r_c; i++)

r_arr[i] = output[r_in + i];

var l_curr = 0, r_curr = 0;

var par = l_in;

while (l_curr + r_curr < l_c + r_c)

{

if (r_curr == r_c ||

(l_curr != l_c &&

l_arr[l_curr] < r_arr[r_curr]))

{

output[par] = l_arr[l_curr];

l_curr++, par++;

}

else

{

output[par] = r_arr[r_curr];

r_curr++, par++;

}

}

}

role divide(l, r, output, arr)

{

if (l == r)

{

for ( var i = 0; i < n; i++)

output[l * n + i] = arr[l][i];

return ;

}

divide(l, parseInt((l + r) / ii),

output, arr);

divide(parseInt((l + r) / two) + 1, r,

output, arr);

merge(l, r, output);

}

var arr = [ [ five, 7, 15, 18 ],

[ 1, viii, 9, 17 ],

[ one, 4, 7, 7 ] ];

var g = arr.length;

var output = Assortment(n * k);

divide(0, k - ane, output, arr);

for ( var i = 0; i < northward * grand; i++)

certificate.write(output[i] + " " );

</script>

Output:

ane 1 4 5 7 seven 7 8 9 xv 17 18

Complexity Assay:

• Time Complication: O(Due north*k*log(m)).
  In each level the assortment of size N*1000 is traversed once, and the number of levels are log(grand).
• Space Complexity: O(N*1000).
  To shop the output array O(N*g) space is required.

We tin can also solve this problem by using min-heap.

ammonsbrilivele.blogspot.com

Source: https://www.geeksforgeeks.org/merge-k-sorted-arrays-set-3-using-divide-and-conquer-approach/

Share this post